If x yy x = 100, then dy/dx is equal to If Xi Greater Than 0 I Equal 1 2 3 N Then X1 Plus X2 Plus 1 By X1 Plus 1 By X2 Plus 1 By Is Equal To If Xy Tan 1 Xy Cot 1 Xy Then Dy Dx Is Equal To If y (t) is solution of (1 t) (dy / dt) ty = 1 and y (0) = 1, then y (1) = If y = (1 x 2) tan1 x x, then dy/dx =In calculus, Leibniz's notation, named in honor of the 17thcentury German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively Consider y as a function of a variable x, or y = f(x) If this is the case, then Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at Teachoo

If Y X X 5 Then Prove That X Dy Dx Y 1 Y
Y=sin(x^x) dy/dx
Y=sin(x^x) dy/dx- If xy = yx, find dy/dx Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesReplies 6 Views 1K Differentiation find dy/dx if y=x^y Last Post;




Solve X Dy Dx Y Y 2logx Youtube
Ex 96, 3 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑑𝑦𝑑𝑥 𝑦𝑥= 𝑥2 𝑑𝑦𝑑𝑥 𝑦𝑥= 𝑥2 Differential equation is of the form 𝑑𝑦𝑑𝑥𝑃𝑦=𝑄 where P = 1𝑥 and Q = x2 Finding integrating factor, IF = e 𝑝 𝑑𝑥 IF = eSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Homogeneous Differential Equation dy/dx = (y x)/(y x)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support
In calculus, the differential represents the principal part of the change in a function y = f(x) with respect to changes in the independent variableThe differential dy is defined by = ′ (), where ′ is the derivative of f with respect to x, and dx is an additional real variable (so that dy is a function of x and dx)The notation is such that the equationExperts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality highSimple and best practice solution for (yx)dy(xy)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it
dy/dx = x yUse substitutionv = x yDifferentiate with respect to xdv/dx = 1 dy/dxdy/dx = 1 dv/dxNow we use above substitutions in differential equationsdy/dx = x y1 dv/dx = vdv/dx = 1Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeY' (a)= (dF (a,b)/dx)/ (dF (a,b)/dy) (a,b) (where dF (a,b)/dx and dF (a,b)/dy standing for the 2 partial derivatives of F (x,y) at (a,b) ) In the case we are talking about, it would be easier to write the equation x^y=y^x as F (x,y)=y*log (x)x*log (y)=0




Solve The Differential Equation X Dy Dx Y Cube X Youtube




Solve Xex Y Y Sin Y X X Dy Dx Sin Y X 0 Maths Differential Equations Meritnation Com
Multiply by y/y first Note from our relation 2y^2\log yx^2=0 that adding x^2 to both sides yields 2y^2\log y=x^2 Substitute for 2y^2\log y and you are done \begin {align*}\frac {dy} {dx}&=\frac {x} {2y\log yy}\\&=\frac {xy} {2y^2\log yy^2}\\&=\frac {xy} {x^2y^2}\end {align*} Multiply by y/y first Note from our relation 2y2 logy− x2 = 0 that adding x2 to both sides yields 2y2logy = x2 We rearrange a little dy dx = x 2y x −y dy dx = 1 2(y x) 1 − (y x) (I) While I may not need to mention this, this differential equation is what is called a homogeneous differential equation I'll discuss this after the work here Knowing that the differential equation is of that type, it tells us that theSee the answer See the answer See the answer done loading Find the derivative of y =√x (x^26) dy/dx= Expert Answer Who are the experts?



How To Solve Dy Dx Tan Y X Y X Quora




Engineering Mathematics Notes
==> dy/dx = (y1)/(1x) Approved by eNotes Editorial Team We'll help your grades soar Start your 48hour free trial and unlock all the summaries, Q&A,Learn how to solve differential equations problems step by step online Solve the differential equation dy/dxy/x=x/(3y) Multiplying the fraction by 1 We identify that the differential equation \\frac{dy}{dx}\\frac{y}{x}=\\frac{x}{3y} is a Bernoulli differential equation since it's of the form \\frac{dy}{dx}P(x)y=Q(x)y^n, where n is any real number different from 0 and 1 To solve thisFree separable differential equations calculator solve separable differential equations stepbystep




If Y X X2 1 1 2 M Then Show That X2 1 D2y Dx2 X Dy Dx M2y 0 Mathematics Topperlearning Com 6jd9kell




1 X Cos Y X Y Sin Y X Y Y Y X X Cos Y X X Gauthmath
E y(x)= 5x 7 In x C y(x)= 5x2 7x In x Cx y(x)= {x} {x} Cx y(x)= {x} {x?Log y = y log x taking differentiation both side with respect to x d/dx (log y) = d/dx (y log x) 1/y*dy/dx = y* d/dx (logx)logx*dy/dx 1/y*dy/dx = y / xlogx*dy/dx dy/dx (1/y logx) = y/x dy/dx = y^2 / x (1 y lox) Thanks & Regards, Nirmal SinghAnswer to Find the general solution to the equation dy y dx Math;




Math 432 Hw 2 5 Solutions Pdf Free Download




If Y X X 5 Then Prove That X Dy Dx Y 1 Y
Explanation We can separate the variables dy dx = y x ⇒ dy y = dx x Integrate both sides ∫ dy y = ∫ dx x ⇒ ln(y) = ln(x) C So y = eln(x)C = eln(x) ⋅ eC = Cx Solve the linear equation dy/dxy/x=x^2 Latest Problem Solving in Differential Equations More Questions in Differential Equations OnlineKCET 19 Permutations and Combinations 3 If 2 x 2 y = 2 x y, then d y d x is KCET 4 Let P = a i j be a 3 × 3 matrix and let Q = b i j where b i j = 2 i j a i j for 1 ≤ i, j ≤ If the determinant of P is 2, then the determinant of the matrix Q is IIT JEE 12 Determinants 5




X Dy Dx Y E X X 0 E Xdy Dx 2e Xy 1 Xy Chegg Com



What Is The Solution Of Homogeneous Differential Equation Dy Dx Y X 2 Y 2 X Quora
Find the general solution to the equation dy y dx Live 3239 5x 7 uck!Yx dy/dx=a(y 2 dy/dx) Dear upendra yx dy/dx=a(y 2 dy/dx) dy/dx (ax)=yay 2 dy/(yay 2 ) =dx/(ax) intigrate both side ∫dy/(yay 2 ) =∫dx/(ax) &in Thank you for registering One of our academic counsellors will contact you within 1 working dayIf y = xx , x > 0 , then (dy/dx) is (A) log x (B) 2 log x xx log x (D) xx ( 1 log x ) Check Answer and Solution for above question from Ma




Answered Find If X Y Y X Dy Dx A 2x 2y Bartleby
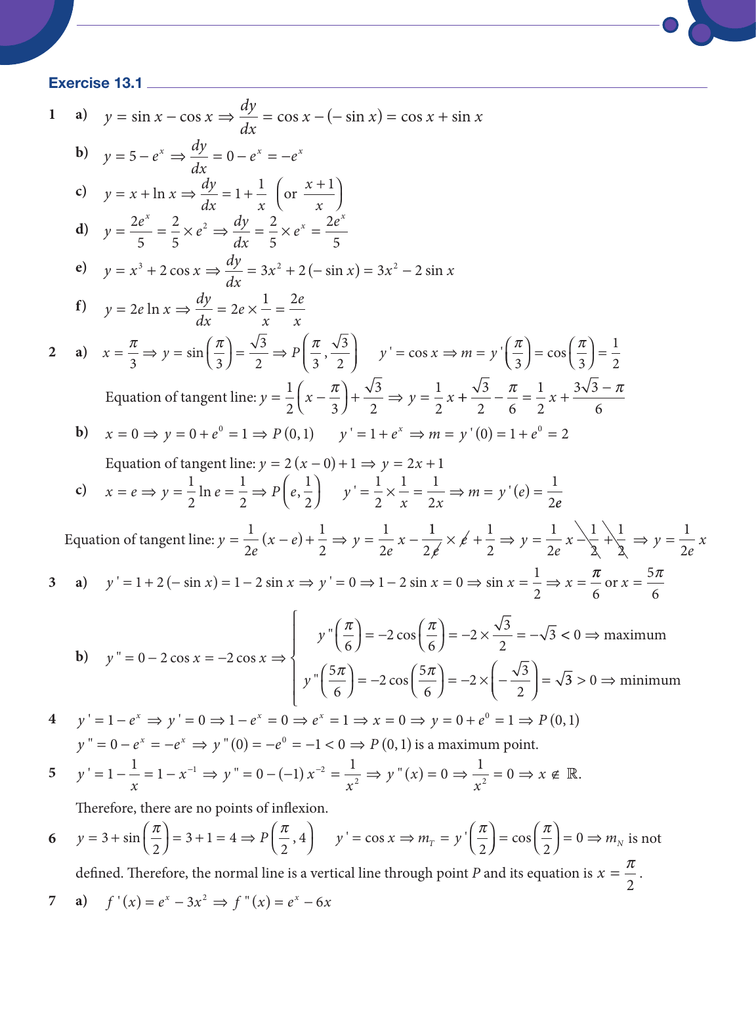



X X Dy Dx X X X X Sin Cos Cos Sin Cos Sin
Advanced Math questions and answers;Get answer If y=x^(x), "find" (dy),(dx) We have, `y=x^(2)` `therefore log y=x log x` On differentiating wrt x, we get `1/y (dy)/(dx)=x/x log Solve the following differential equations \(\frac{dy}{dx}\frac{y}{x}=x^3\) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




If Y X 5 Show That X Dy Dx 5y 0 Youtube




Solve X Dy Dx Y Y 2logx Youtube
Find dy/dx y=3^x y = 3x y = 3 x Differentiate both sides of the equation d dx (y) = d dx (3x) d d x ( y) = d d x ( 3 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate using the Exponential Rule which states that d dx ax d d x a x is axln(a) a x Solve the homogeneous ODE dy/dx = (x^2 y^2)/xy this is pretty easy for me to solve, no doubt on that My question is on the constant Alternatively, is it correct to have, C, then work it from there secondly, we are 'making" , is it for convenience purposes?, supposing i left the constant as it is, would that be wrong?Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of the equation (i), we have ∫ 1 y d y = ∫ 1 x d x




Solve The Differential Eq X Dy Dx Y X Xy Cotx 0 Maths Differential Equations Meritnation Com




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic
Click here👆to get an answer to your question ️ If y = x^x , then find dydxFind dy/dx y=e^x y = ex y = e x Differentiate both sides of the equation d dx (y) = d dx (ex) d d x ( y) = d d x ( e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate using the Exponential Rule which states that d dx ax d d x a x is axln(a) a x ln ( a) where a a = e e ex e x #1 Find y 0 so that the integral curve for dy/dx=xy y (4)=y 0 is a straight line You must justify your answer, which will require you to apply algebraic reasoning to the problem I know the answer is 3 I also know this differential equation looks simple, but I can't get the starting equation separated
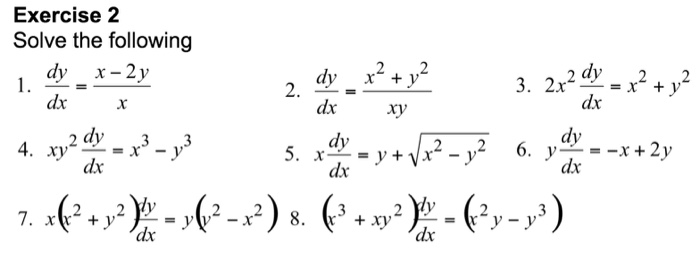



Solve The Following Dy Dx X 2y X Dy Dx X 2 Chegg Com



Solved Solve The Following Bernoulli Equations B 2 X 2 Dy Dx Xy X 3 Y 3 C Y X Y X2 5 X 2 Y 1 2 D X Dy Dx 6y 3xy Course Hero
ডিফারেনশিয়াল সমীকরণ সমাধান `y cos\ y/x (x dyy dx)xsin\ y/x (x dy y dx) = 0` যা সন্তুষ্ট `yReplies 3 Views 2K Solve dx/y = dy/x Last Post;Replies 4 Views 1K L If dy/dx = x^x , find y ?




Solve The Following Differential Equation 1 1 3 Y X Dy Dx Y 3 X 1 2 Ln X Y X Dx Ln X Dy 3 X 2 Y 2 Y 4sin X Dx 2xy 4y 3cos X Dy 4 Tan X 8sin X Sin Y Dx 8cos X Cos Y Dy 0 5 1 Y 2sin 2x Dx Ycos 2x Dy 0 Wegglab




Solve The Differential Equation 2 Dy Dx Y X Square Y X Youtube
Solve dy/dx = x/y , y(0) = 3 Differential equations A differential equation is any equation which contains a function and one or more of it's derivatives The solution to a differentialSolution Given y = x x Take log on both sides log y = x log x Differentiate wrtx (1/y)dy/dx = x (1/x) log x = 1 log x dy/dx = y (1 log x) = x x (1 log x)The following shows how to do it Step 1 First we multiply both sides by d x dx dx to obtain d y = f ( x) d x dy=f (x)~dx dy = f (x) dx Step 2 Then we take the integral of both sides to obtain



How To You Find The General Solution Of Dy Dx X Y Socratic



How To Solve The Equation Dy Dx 1 X Y X Y Quora
Simple and best practice solution for (x^2y^25)dx(yxy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itIn this differentiation problem, the variable y represents a function in x Hence, it can be differentiated with respect to x and do not think that y is a constant Therefore, the function y can be differentiated by the derivative rule of logarithms 1 y × d y d x = d d x Dy/dx ( y/x ) = x(y^3) Last Post;




Find The General Solution Of The Following X Dy Dx 3y X 3 X Y Homeworklib
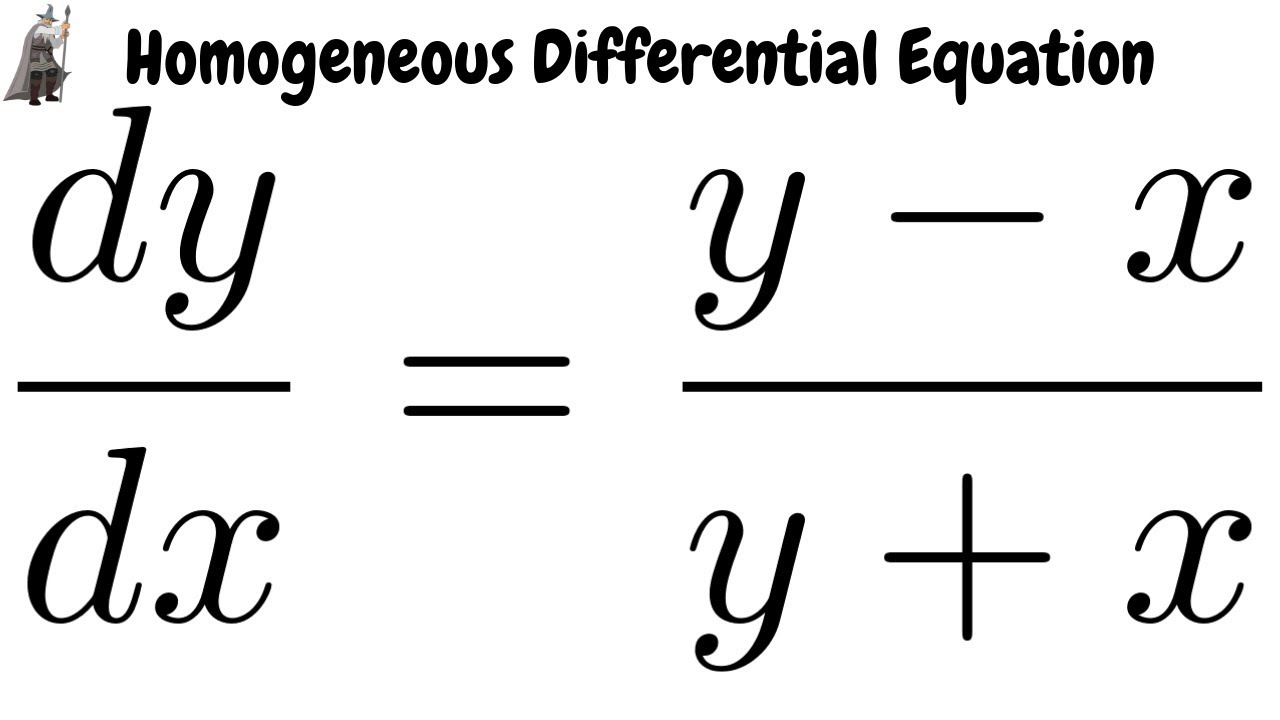



Solving The Homogeneous Differential Equation Dy Dx Y X Y X Youtube
5) d dx x x x () 10 10 1 g32 g16 6) If y = log x then dy dx = 1 x 7) If y = e 2 then dy dx = 2e 8) The derivative of a x is a xloga 9) The derivative of x m y n = (xy) (mn) is x y QIV Solve the following 1) If y = (6 x 3 − 3 x 2 −9 x) 10, find dy dx 2) If y = 3 8 5 2 4 5 x x g14 g14 g11 g12, find dy dx 3) If y = log(log(logx)) 2So we get (1/y)(dy/dx) = log(2) 4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx Recall y=2^x (from our original question)This problem has been solved!



1




Ex 9 6 5 Find General Solution Cos2 X Dy Dx Y Tan X
Implicit\derivative\\frac{dx}{dy},\e^{xy}=e^{4x}e^{5y} implicitderivativecalculator en Related Symbolab blog posts High School Math Solutions – Derivative Calculator, Trigonometric Functions In the previous posts we covered the basic algebraic derivative rules (click here to see previous post) But howUse properties of logarithmic functions to expand the right side of the above equation as follows ln y = x ln x We now differentiate both sides with respect to x, using chain rule on the left side and the product rule on the right y ' (1 / y) = ln x x (1 / x) = ln x 1 , where y ' = dy/dxA first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx




If Y X What Is Dy Dx Quora
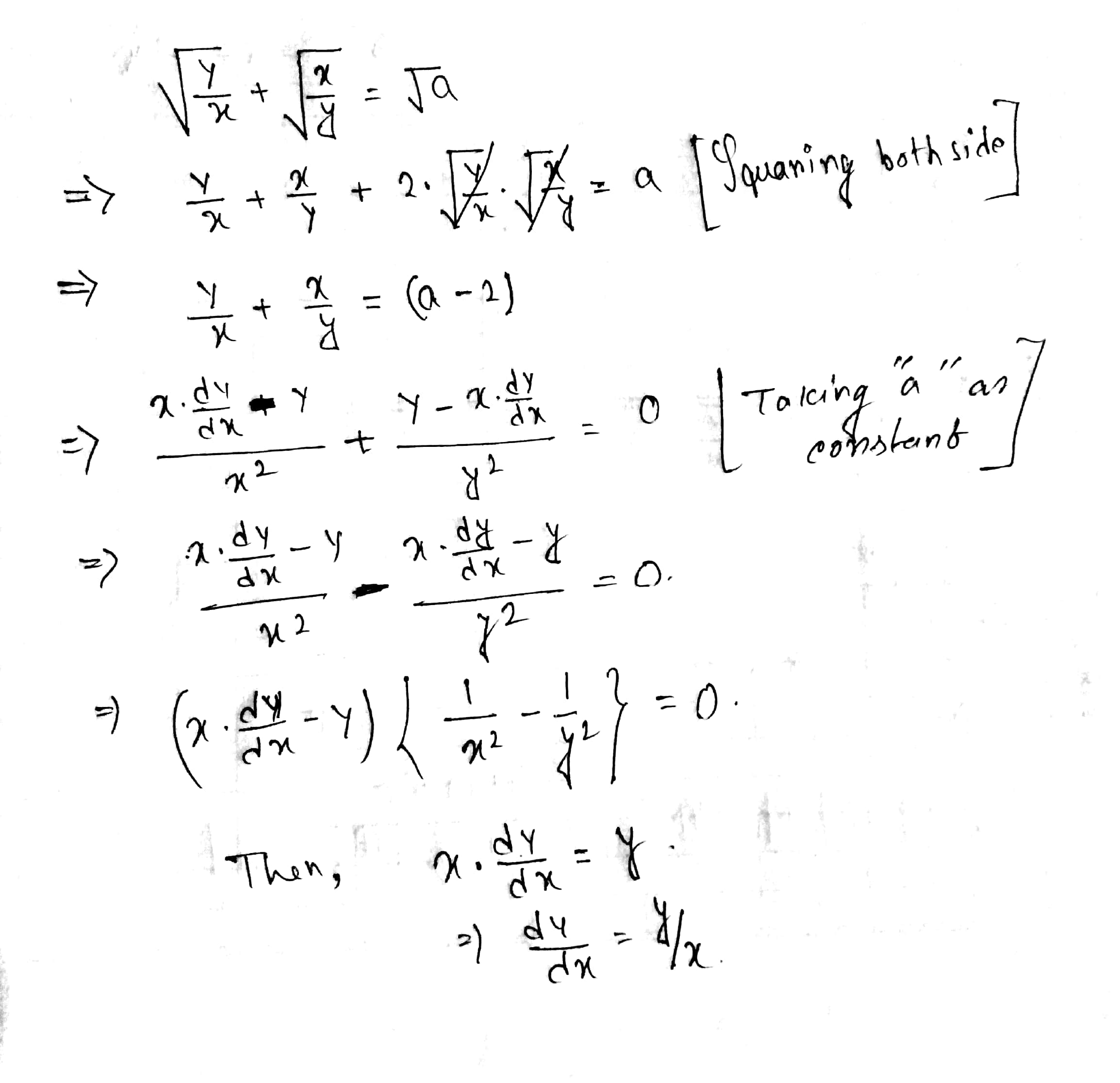



What Is Dy Dx Of Sqrt Y X Sqrt X Y Sqrta Socratic
Dy/dx y/x = logx /x It is a linear differential equation form So, IF (Integration Factor) = e^∫ 1/x dx = e^logx = x Then, =>y×IF = ∫ logx /x × IF dx =>xy = ∫ logx /x × x dx =>xy = ∫ logx dx By using Integration by part in RHS,we getReplies 11 Views 2K Solving dy/dx=xy Last Post;Learn how to solve differential equations problems step by step online Solve the differential equation dx/dy=(x^2y^2)/(1x) Group the terms of the differential equation Move the terms of the x variable to the left side, and the terms of the y variable to the right side Simplify the expression \frac{1x}{x^2}dx Simplify the fraction by x




Ex 9 5 8 Show Homogeneous X Dy Dx Y X Sin Y X 0




Solve Y Xdy Dx A Y 2 Dy Dx
In Introduction to Derivatives (please read it first!) we looked at how to do a derivative using differences and limits Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Tutorial 4 Question For Solution By Substitutions Studocu




Solve Dy Dx 1 X Y Solve Dy Dx Y X 1 Y Solve The Chegg Com




Homogeneous Differential Equations




Teacloocom Dy 2 Sin2 1 R Dsin Y V Dy Dx Dy Y Cos Y X 2 Sin Dx Calculating Derivative Of Cos Xy Dcosxy Sinxy 은 Xy X Ax Dy
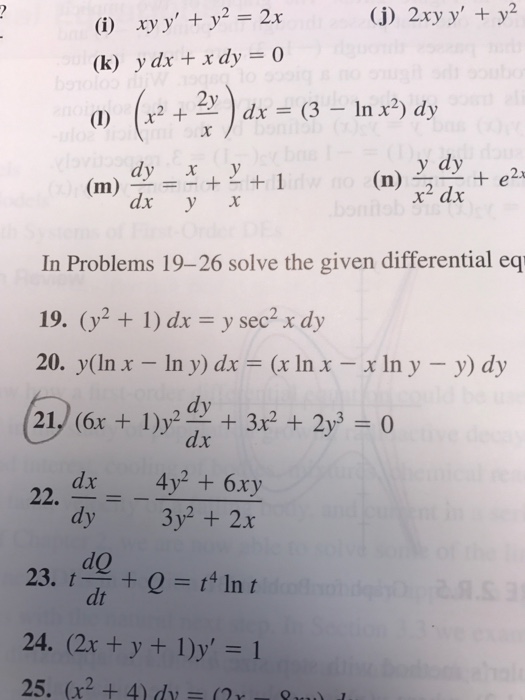



Xy Y Y 2 2x 2xy Y Y 2 Y Dx X Dy 0 X 2 Chegg Com




Linear Differential Equation X Dy Dx Y X 2sin X With Transient Terms And Interval For Solution Topic Play




Engineering Mathematics Notes




Given That Y X X Y Wich Of The Following Expressions Equal Dy Dx Brainly Com




The General Solution Of X Dy Dx Y X Tan Y X Is Youtube




Solution Solve The Linear Equation Dy Dx Y X X 2




Engineering Mathematics Notes




If Y X Sin Y Prove That X Dy Dx Y 1 X Cos Y Mathematics Topperlearning Com Tz9vph66




Differential Equations Separation Of Variables Ppt Download




Solve The Differential Equation X Dy Dx Y X Cosx Sinx Given That Y Pie 2 1 Maths Differential Equations Meritnation Com



1



Www Tau Ac Il Levant Ode Solution 6 Pdf



If Y X X 2 Prove That X Dy Dx 1 Y Y Sarthaks Econnect Largest Online Education Community




Differential Equations Solved Examples Dy Dx Y X




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection



Solve X Dy Dx Y Log Y Log X 1 Studyrankersonline



1




Dy Dx X2 Y2 2xy Novocom Top




C4 Chapter 6 Integration Ppt Download




Homogeneous Differential Equations




If Y X X 5 Prove That X Dy Dx Y 1 Y Maths Limits And Derivatives Meritnation Com




Dy Dx X Y 1 X Y 3 Novocom Top




Math 432 Hw 2 4 Solutions



How To Graph X 2 Dy Dx Y Xy Y 1 1 Quora



Find The Particular Solution Of The Differential Equation X Cos Y X Dy Dx Y Cos Y X X Given That When X 1 Y Pi 4 Sarthaks Econnect Largest Online Education Community




Bernoulli Equation For Solving Differential Equation Dy Dx Y X X 2y 2 Youtube




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert




Linear Differential Equation X Dy Dx Y X 2sin X With Transient Terms And Interval For Solution Topic Play




Show That The Given Differential Equation Is Homogeneous And Solve X Dy Dx Y X Sin Y X 0 Mathematics Shaalaa Com



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora




Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com
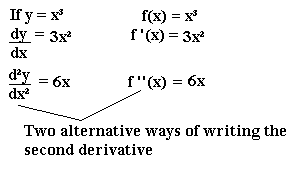



The Second Derivative Mathematics A Level Revision




Solution Solve The Linear Equation Dy Dx Y X X 2



Differential Equation Help D2jsp Topic




If Y X 1 X Show That 2x Dydx Y 2 X




Show That The Given Differential Equation Is Homogeneous And Solve X Dy Dx Y X Sin Y X 0 Mathematics Shaalaa Com




Solve The Following Differential Equation 1 1 3 Y X Dy Dx Y 3 X 1 2 Ln X Y X Dx Ln X Dy 3 X 2 Y 2 Y 4sin X Dx 2xy 4y 3cos X Dy 4 Tan X 8sin X Sin Y Dx 8cos X Cos Y Dy 0 5 1 Y 2sin 2x Dx Ycos 2x Dy 0 Wegglab



Solve The Following Differential Equation X Dy Dx Y X Tan Y X Sarthaks Econnect Largest Online Education Community




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Solve The Differential Equation X Dy Dx Y Xe X Chegg Com



If X Y Y X What Is Dy Dx Quora




Solve The Following X Dy Dx Y X 2 Dy Dx 2y Chegg Com




X Dy Dx Y X 3 Given That Y 1 When X 2




Find The General Solution Of Y 2y 5 3 5 X Dy Dx Gauthmath




Find Dy Dx For The Following 1i Y Ln Frac X Square Gauthmath




The Differential Equation X Dy Dx Y X 3 Has The General Solution Youtube




Bernoulli Differential Equation X Dy Dx Y 1 Y 2 Topic Play




If Y Sinx X Then Dy Dx



If Y X Is A Solution Of 2 Sinx 1 Y Dy Dx Cosx And Y 0 1 Then Find The Value Of Y P 2 Studyrankersonline




Ex 9 6 3 Find General Solution Dy Dx Y X X2 Ex 9 6




4 Solve The Differential Equation Y X Dy Dx Gauthmath



If Y X X 5 Then Prove That X Dy Dx Y 1 Y Sarthaks Econnect Largest Online Education Community




Math 432 Hw 2 5 Solutions




Solve The Differential Equations In Exercises 1 14 Chegg Com




Resonance Aieee Iit Study Material Maths Complete Pdf By S Dharmaraj Issuu




X Dy Dx Y X Cos 2 Y X Youtube




Solve X Dy Dx 2 Y X Dy Dx Y 0




Differential Equation 1st Order Sol 6 Of 10 Exact Differentials Ex 5 1 X Dy Y X 2 Dx 0 Youtube




Y 2xy E X Dx E Xdy 0 Novocom Top




Find Dy Dx If Y X Cot 1 X Y Brainly In



Search Q Dy Dx Examples Tbm Isch




Engineering Mathematics Notes




Math 432 Hw 2 4 Solutions Frostburg




Math 432 Hw 2 5 Solutions Pdf Free Download




Example 33 Find Dy Dx If Y X X Y X X A B Teachoo




Y X Cot Y X Dx Xdy 0 Novocom Top




If Y X X 4 Prove That X Dy Dx Y Y 1 0




Solve The Following Differential Equation Given That Y 1 When




Practice Questions Calculus Xii



0 件のコメント:
コメントを投稿