This page includes a sample of a lesson plan I created and implemented, as well as a recorded lesson and correlating selfreflection These are taken from my student teaching semester in a 7th grade math classroom 1 This allows you to reflect the function on an arbitrary line and without being restricted in your choice of compilers a=b=1 is the x=y line \documentclass tikz,border=314mm {standalone} \usetikzlibrary {backgrounds} \begin {document} \begin {tikzpicture} declare function= { f (\x) = 2*\x*\x*exp (2*\x1);The reflective cycle model by Gibbs (19) allows the users to systematise their past experiences, emotions, and findings in the manner supporting future learning and development It includes six consecutive phases that I will use to explore the selected issue more indepth in the following subsections Figure 1 Gibbs' Reflective Cycle

Reflecting Functions Examples Video Khan Academy
How to do a reflection of y=x
How to do a reflection of y=x-Reflection Examples C# This example shows how to dynamically load assembly, how to create object instance, how to invoke method or how to get and set property value Create instance from assembly that is in your project References The following examples create instances of DateTime class from the System assemblySelfreflection assignment Discussion using Gibbs Cycle Question Task Write a report on selfreflection assignment reflecting on the novel value proposition using Gibbs reflective cycle Answer Introduction Thisselfreflection assignment helps in understanding the manner in which a particular project has been prepared




Transformations Boundless Algebra
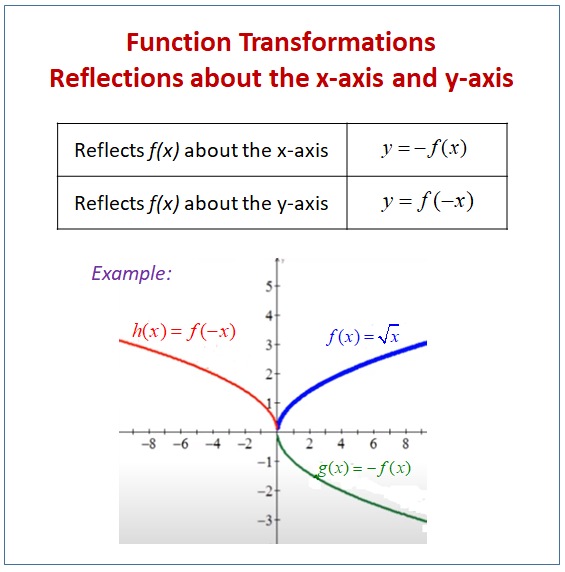
Learn more about Reflection (Visual Basic) In this article Reflection provides objects (of type Type) that describe assemblies, modules and typesYou can use reflection to dynamically create an instance of a type, bind the type to an existing object, or get the type from an existing object and invoke its methods or access its fields and properties Learn about and revise how to apply transformations such as reflections and shifts to graphs with GCSE Bitesize OCR Maths For example, \(y = x^3 2\) is a translation of \(y = The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)
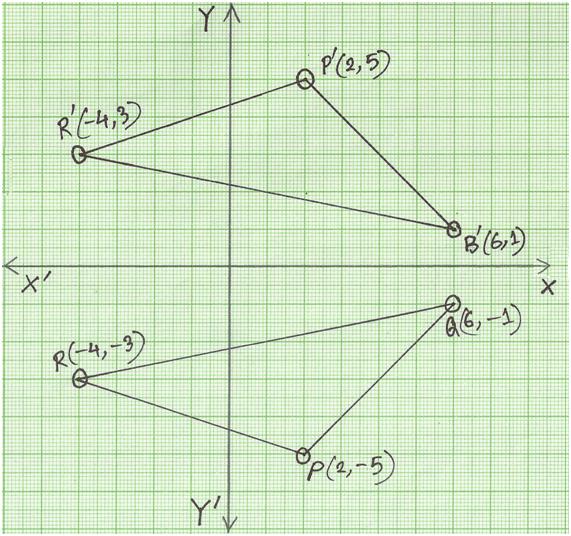
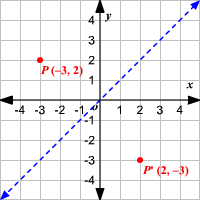
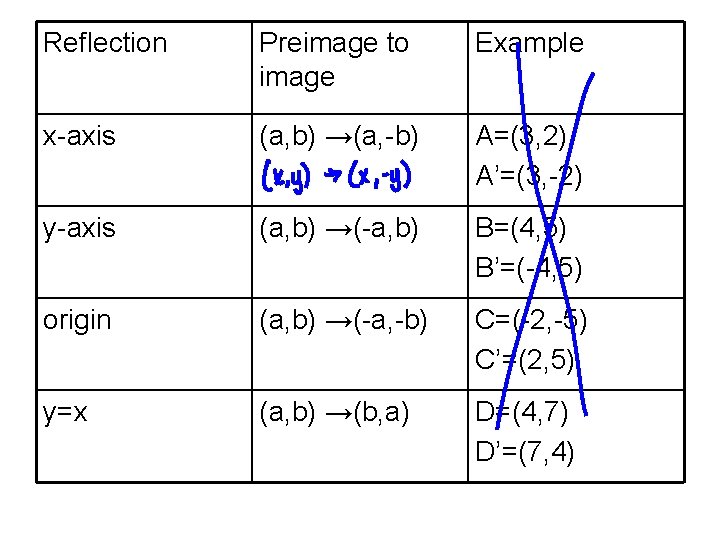
Y=x reflection The rule for a reflection over the y axis is x y x y Common Reflections About the Origin A reflection of a point over the y axis is shown First of all the object is rotated at 45 Example 1 – reflection a linear function across the line y x The last step is the rotation of yx back to its original position that isAn overview of the Reflections Example included with UE4Y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) the line y = x is the point (y, x) the line y = x is the point (y, x) Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure
Reflection in the line y = x A reflection of a point over the line y = x is shown The rule for a reflection in the line y = x is ( x , y ) → ( y , x )"Teaching Experience Reflection" with % discount!4 Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxis The last step is the rotation of y=x back to its original position that is counterclockwise at 45°




Reflections Read Geometry Ck 12 Foundation



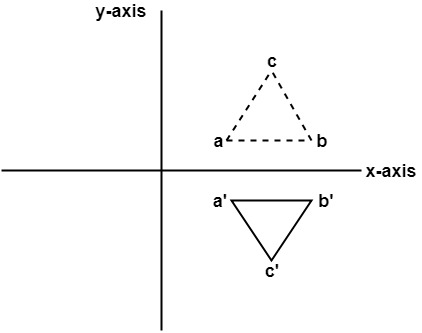
Reflection Of A Point In X Axis Reflection Of A Point Reflection
Let $\theta$ be the angle between $y=x1$ and $x=1$, and let $m_1, m_2$ be the slopes of the lines $y=x1$ and $x=1$ respectively Now we define a slope $m_3$, which will become the slope of the reflected line Since angle of incidence equals angle of reflection, we have the following equation necessarily Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change sizeExample 5 2 Reflection Reflection Over Y X In order to define or describe a reflection you need the equation of the line of reflection If a b is reflected on the line y x its image is the point b a Geometry Reflection A reflection is an isometry which means the original and image are congruent that can be described as a flip



How To Reflect A Graph Through The X Axis Y Axis Or Origin



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Reflection in the Line y = x Matrix Reflection in the yaxis Matrix Reflection Assignment – GeoGebra Triangle Reflection across X=1 – GeoGebra Solved SOLVING The Diagram Below AB Is The Image Of Aß Af Even and Odd Functions Mathematics ABC is reflected to form A'B'C'Pick Reflection Questions Answer Your Reflection Questions Read your questions, understand them, then embark on answering them This does not necessarily have to be in perfect sentence or formal essay form Your aim should be to gather as many ideas as possible Identify What Your Experiences Mean What Is an Example of Reflection?



1



1
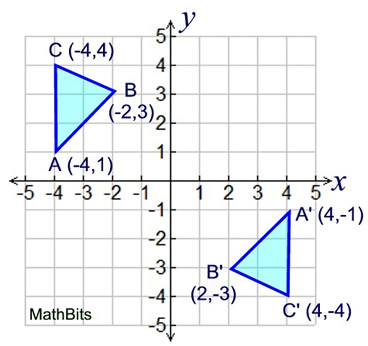
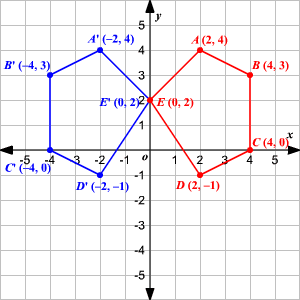
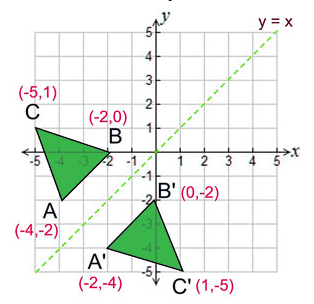
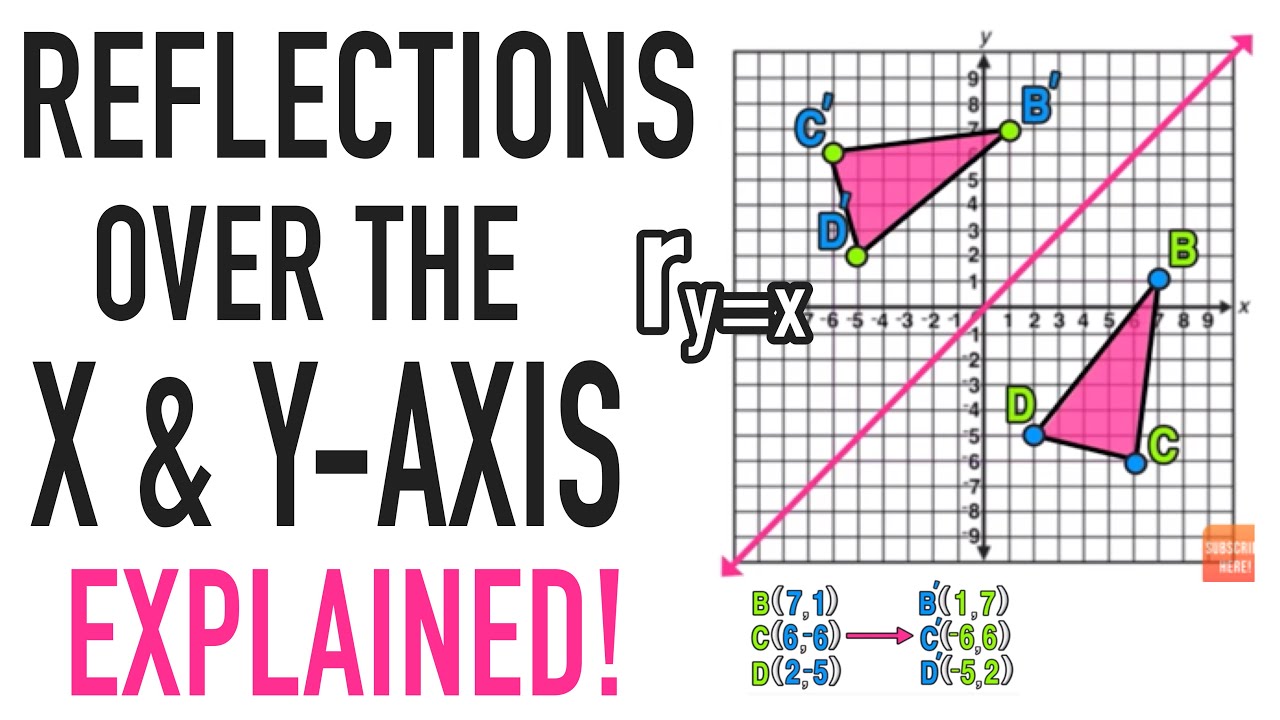
We need an m x n matrix A to allow a linear transformation from Rn to Rm through Ax = b In the example, T R2 > R2 Hence, a 2 x 2 matrix is needed If we just used a 1 x 2 matrix A = 1 2, the transformation Ax would give us vectors in R1 For example, when reflecting the point (2,5) over y=x it becomes (5,2) This is very simple, but why does it work? The reflected image has the same size as the original figure, but with a reverse orientation Examples of transformation geometry in the coordinate plane Reflection over y axis (x, y) ( xWhen reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x = (y,x) For example For triangle ABC




Reflection Key Stage 2



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com
Creative Communication This reflective essay example about the topic of creative writing is what you might expect to see at the college level I've always felt I excel in written communication The skill of effectively communicating my thoughts and feelings through words and expressions seemed to come easily to meReflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Students with a visual preference, for example, will work better in activities such as creating a personal life timeline By contrast, a student with an auditory preference will likely be more productive in a



Geometry Reflection




Reflect Function About Y Axis F X Expii
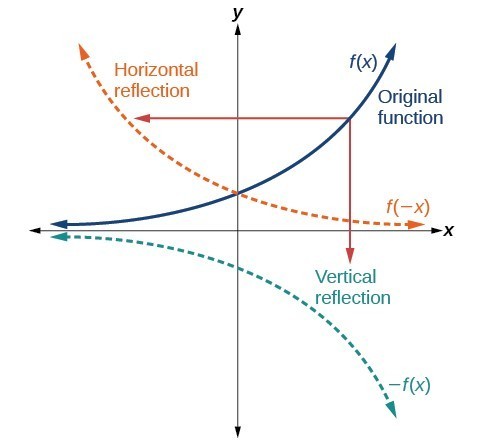
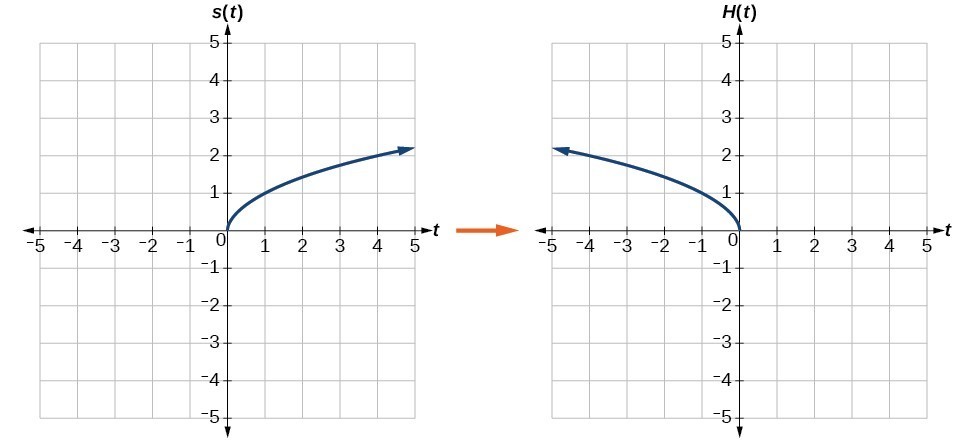
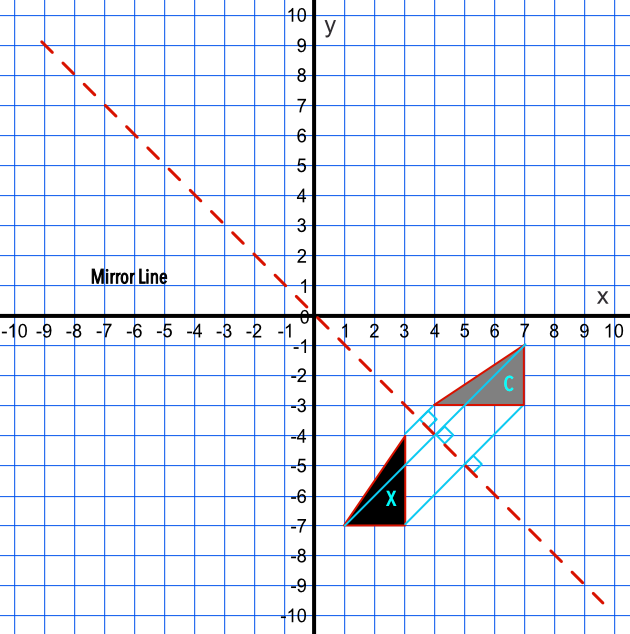
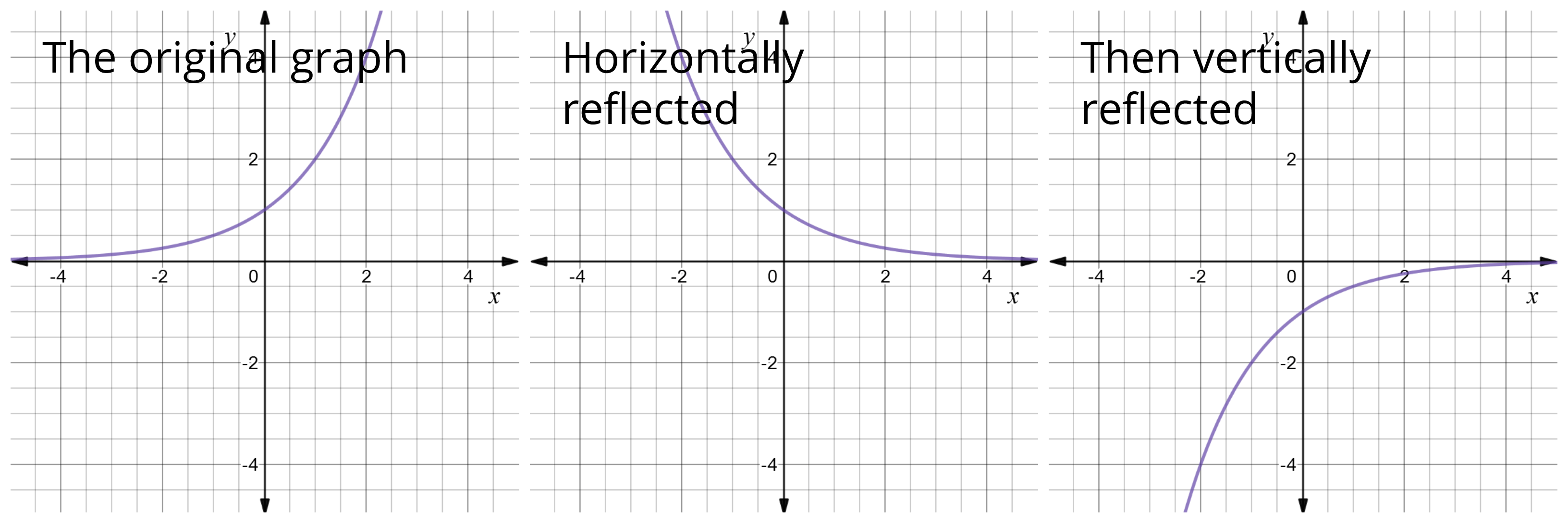
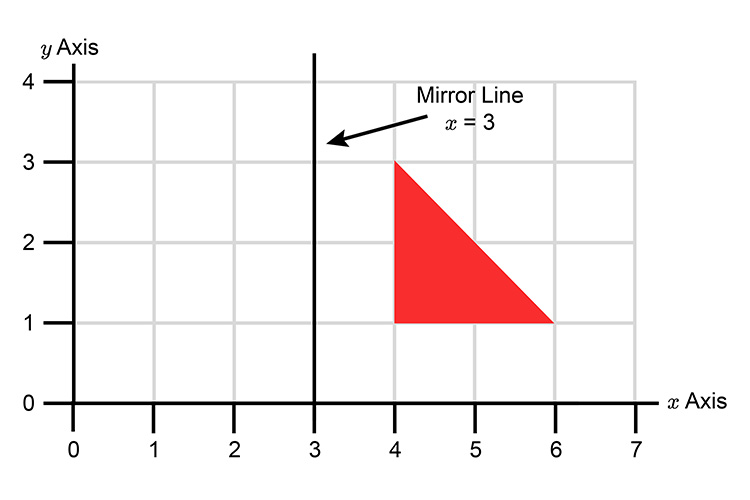
In a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3Example 7 Reflecting a Graph Horizontally and Vertically Reflect the graph of latexs\left(t\right)=\sqrt{t}/latex (a) vertically and (b) horizontally Solution a Reflecting the graph vertically means that each output value will be reflected over the horizontal tReflection in yaxis is given by M y (x, y) = (x, y) A' = Reflection of A(4, 1) in yaxis = (4, 1) Reflection in xaxis is given by M x (x, y) = (x, y) B' = Reflection of B in x




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative
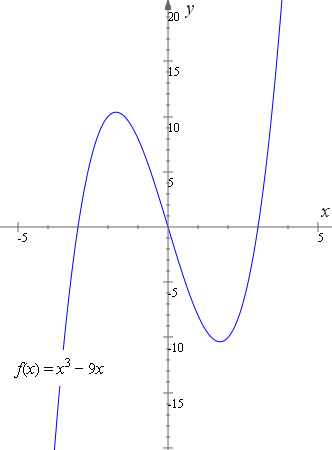
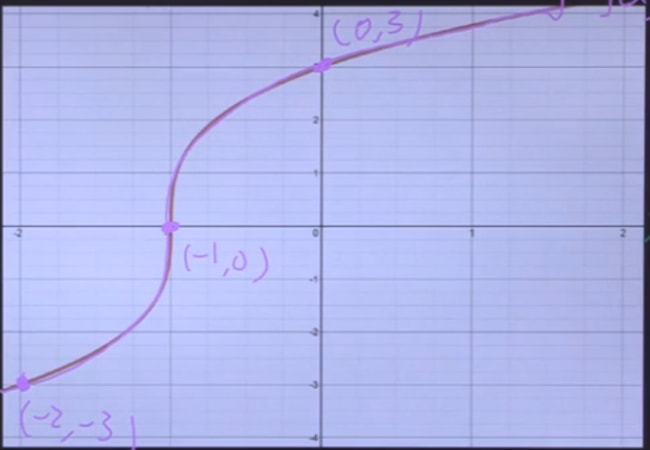
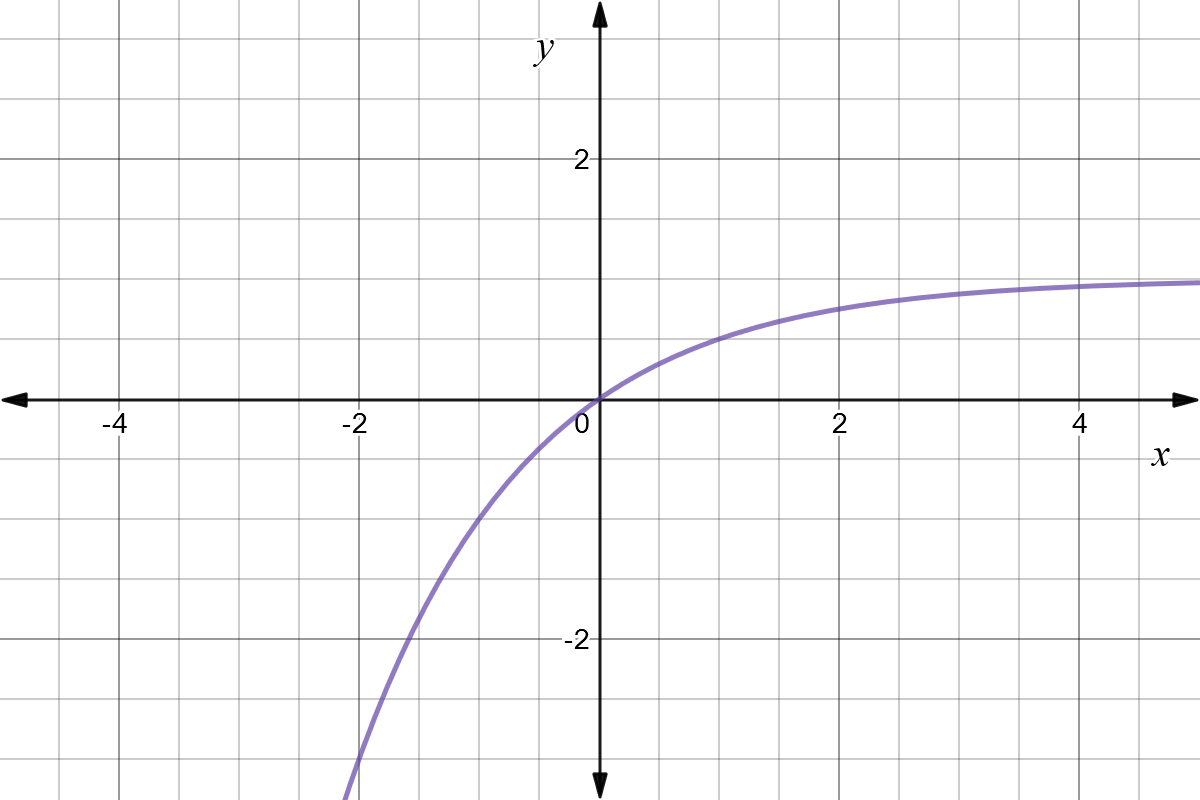
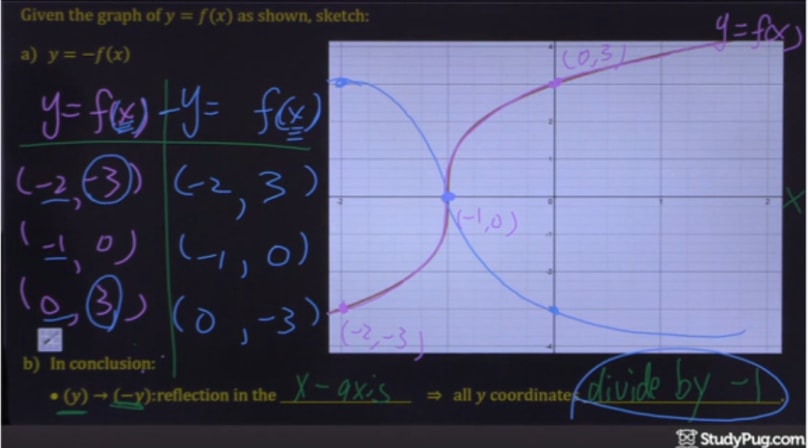
Reflection Transformations in 2Space Let such that and suppose that we want to reflect across the axis as illustrated Thus the coordinate of our vector will be the opposite to that of our image The following equations summarize our image Thus our standard matrix is , and in form we get that Of course there are other types of reflectionRelated Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?Some useful reflections of y = f (x) are (i) The graph y = −f (x) is the reflection of the graph of f about the xaxis (ii) The graph y = f (−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x Translation A translation of a graph is a vertical or



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
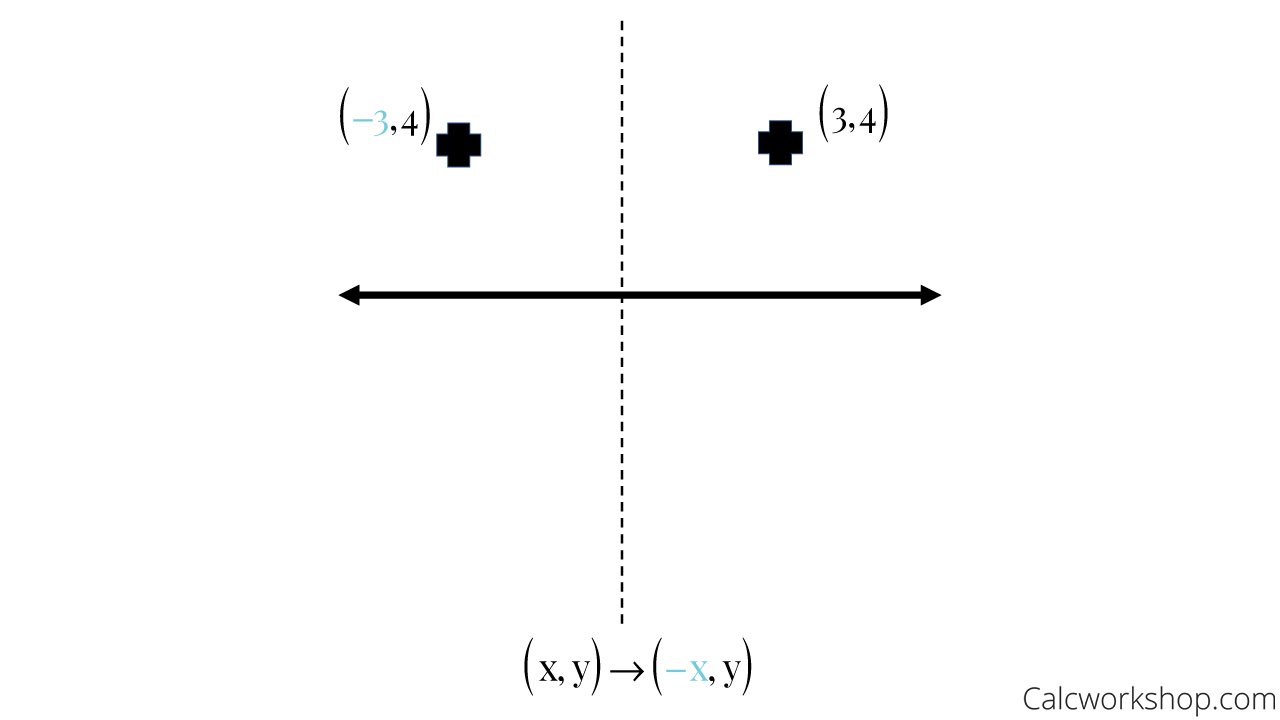



Reflection Rules How To W 25 Step By Step Examples
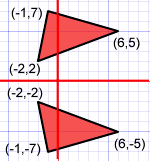
Reflection across y=x example What does reflection across y=x mean This lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitterY= x The reflection of (x, y) is (y, x) R(–2, 2 ) R'(2, –2) S(5, 0 ) S'Reflection X seamlessly integrates UNIX applications and Windows desktops For example, you can easily launch a graphical UNIX application using a desktop shortcut;It is easier to understand reflection with an example The diagram below shows a reflection of a shape The shape before the reflection (called the object) is in light blue The shape after the reflection (called the image) is in dark blue In this example, the shape has reflected in a line of reflection (shown as a red dashed line) on the yaxis




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflection Definition Reflection In The Coordinate Plane
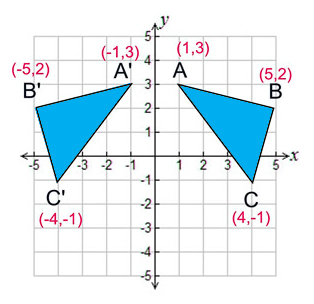
Course Reflection Sample 1 This course has been a great source of learning for me There are many dimensions of learning that I had from this course First is the fact that I have had to discuss different topics in the discussion area which proved to be vital for me and was a great experience for me Especially there was a lot to learn about Reflection of point X, Y is Y, X in the case of line Y = X Reflection of point X, Y is Y, X in the case of line Y = X Gist about Reflection on a Point The point of reflection is also referred to as the centre of a figure Any structure is built using this reflection point asA reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = x (A, B) → (B, A)




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Lesson Explainer Function Transformations Reflection Nagwa
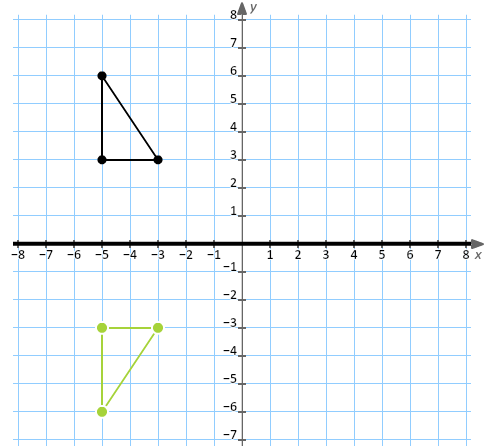
%< enter your function rightTriangle DEF is formed by reflecting ABC across the yaxis and has vertices D (4, 6), E (6, 2) and F (2, 4) All of the points on triangle ABC undergo the same change to form DEF Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x)How do you solve reflections?




Gch12 L1




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
A) x = 6 Whether you are reflecting on, for example, an activity, book/newspaper, or academic essay, you want to highlight key ideas and concepts You can start writing your reflection paper by summarizing the main concept of your notes to see if your paper includes all the information needed for your readersReflections worksheet properties axis graph triangle algebraic reflection line onlinemath4all its Graphing Example Reflecting Across the yaxis and which graph represents a reflection of f(x) = 2(04)x Reflection over y=x Reflections across y=x – GeoGebra What is the equation for the line of reflection?




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities




Transformations Boundless Algebra
The UNIX application appears to be running in Windows You can minimize, maximize, restore, and close your UNIX application just like you can with a Windows applicationThis is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendable



Ch 3 4




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Transformations Of Graphs




Reflecting Functions Examples Video Khan Academy



1




Reflection Rules How To W 25 Step By Step Examples




Line Of Reflection Y 0 Novocom Top




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Reflection Rules How To W 25 Step By Step Examples



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Reflections Across Y X Geogebra



Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf




Reflection Over Y X Math Geometry Showme



Reflection An Isometry Or Rigid Motion In Which A Figure Is Flipped Giving Its Image An Opposite Orientation Ppt Download



How To Reflect A Graph Through The X Axis Studypug




Reflection Over The Line Y X Youtube




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Ppt Lesson 9 1 Powerpoint Presentation Free Download Id 3473



Reflection



Reflection Mathbitsnotebook Jr




Lesson Transformations Lesson 10 5 Transformations 1 Types



Chapter 8 Page 460




Reflection Transformation Matrix




Reflection Rules How To W 25 Step By Step Examples
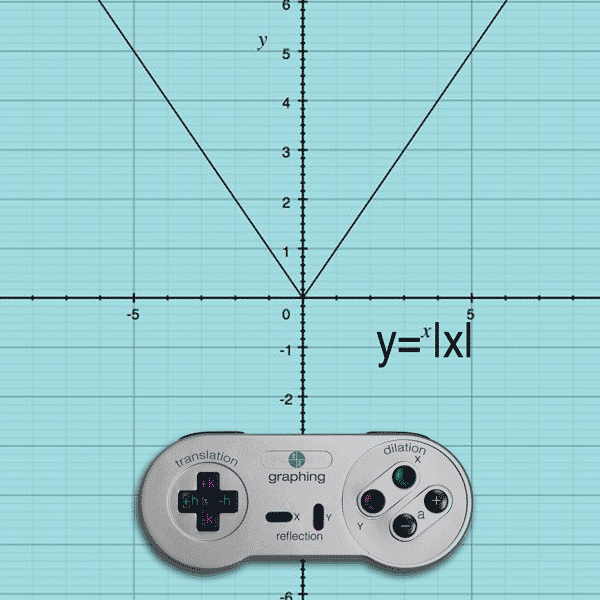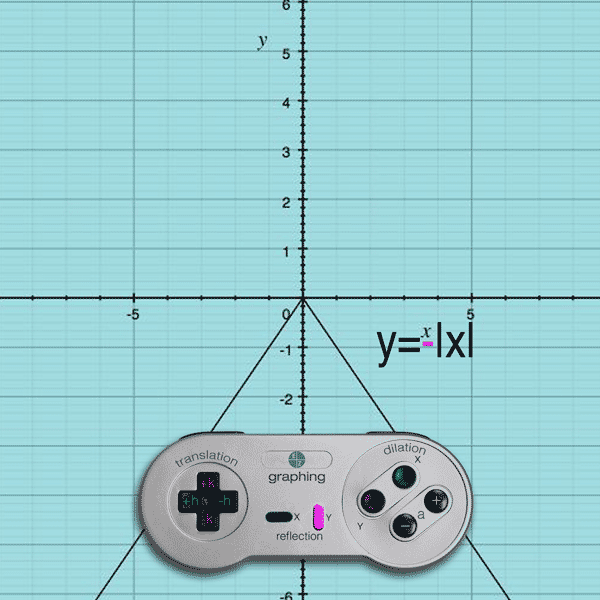



Reflections Ez Graphing




Transformation Reflection Over The Line Y X Youtube



Reflection Over The X And Y Axis The Complete Guide Mashup Math
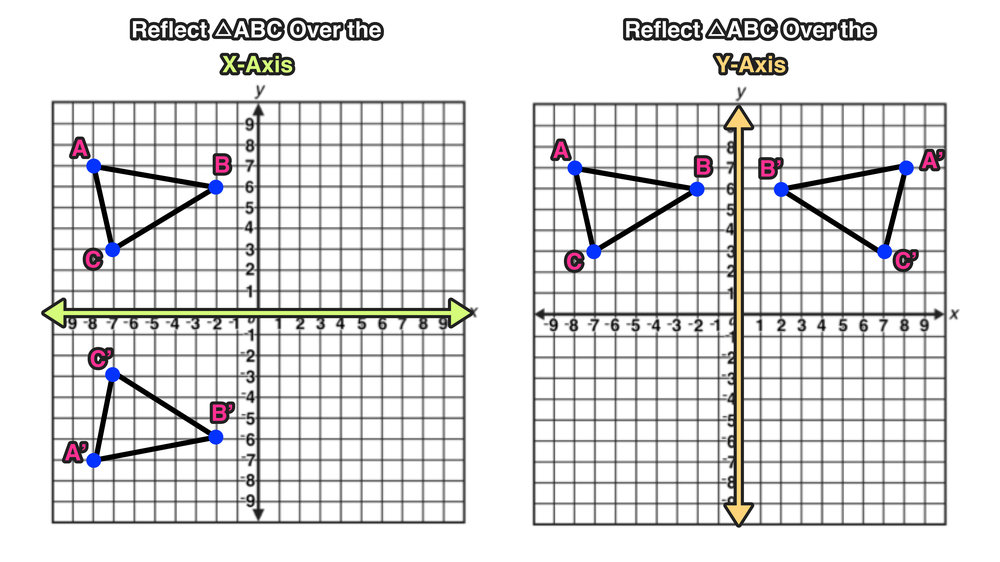



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflect Function About Y Axis F X Expii




Content Transformations Of The Parabola




Reflection Worksheets



How To Reflect A Graph Through The X Axis Studypug




9 2 Reflections Key Concepts R Stands For Reflection And The Subscript Tells You What To Reflect On Ex R X Axis The Line Of Reflection Is What Ppt Download




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Transformation Matrix



2



Reflections



1 5 Shifting Reflecting And Stretching Graphs



Reflect Function About Y Axis F X Expii



Transformation Of Graphs Using Matrices Reflection



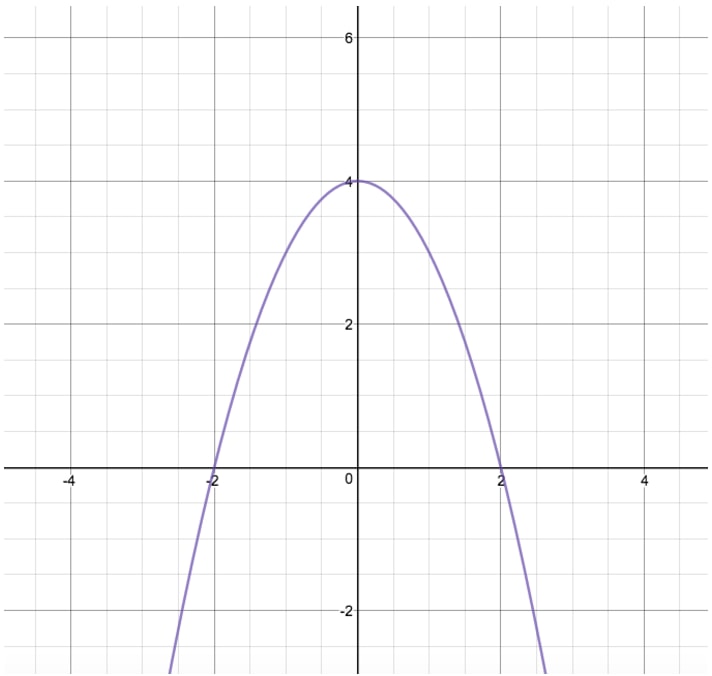
Quadratic Function




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflection In A Cartesian Plane Lexique De Mathematique




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Computer Graphics Reflection Javatpoint




Translations Rotations And Reflections Ck 12 Foundation




Describe How A Reflection Across The Y Axis Affects Each Point On A Graph Give An Example To Illustrate Your Answer Homework Help And Answers Slader




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Reflection Mathbitsnotebook A1 Ccss Math




Solution Example 1 Find The Image Of A Glide Reflection The Vertices Of Abc Are A 3 2 B 6 3 And C 7 1 Find The Image Of Abc After The Glide Reflection Ppt Download




Picture Of Reflection Across Y Axis Reflection Math Transformations Math Math



Reflection Of A Point In X Axis Reflection Of A Point Reflection



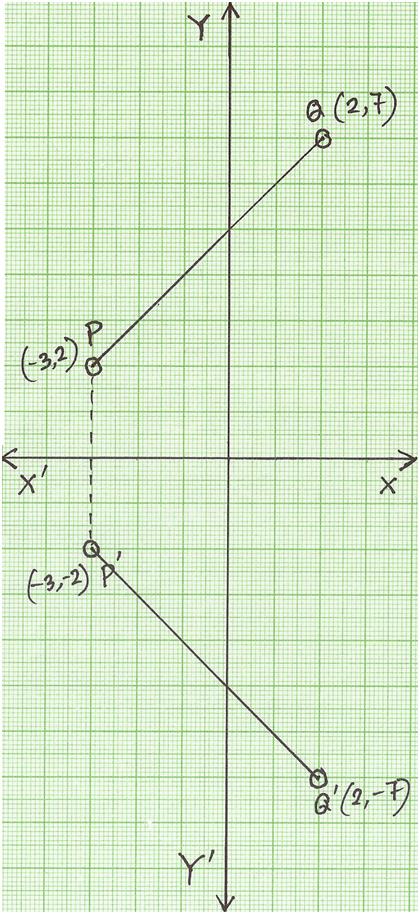
Reflection Definition Reflection In The Coordinate Plane




Reflection Mathbitsnotebook A1 Ccss Math
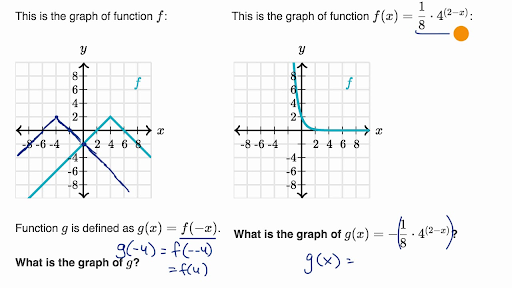



Reflecting Functions Examples Video Khan Academy



How To Reflect A Graph Through The X Axis Studypug



9 1 Reflections Definitions Preimagethe Shape Before It



How To Reflect A Graph Through The X Axis Studypug




Reflection Transformation Matrix



Reflections Over The X Axis And Y Axis Explained Youtube
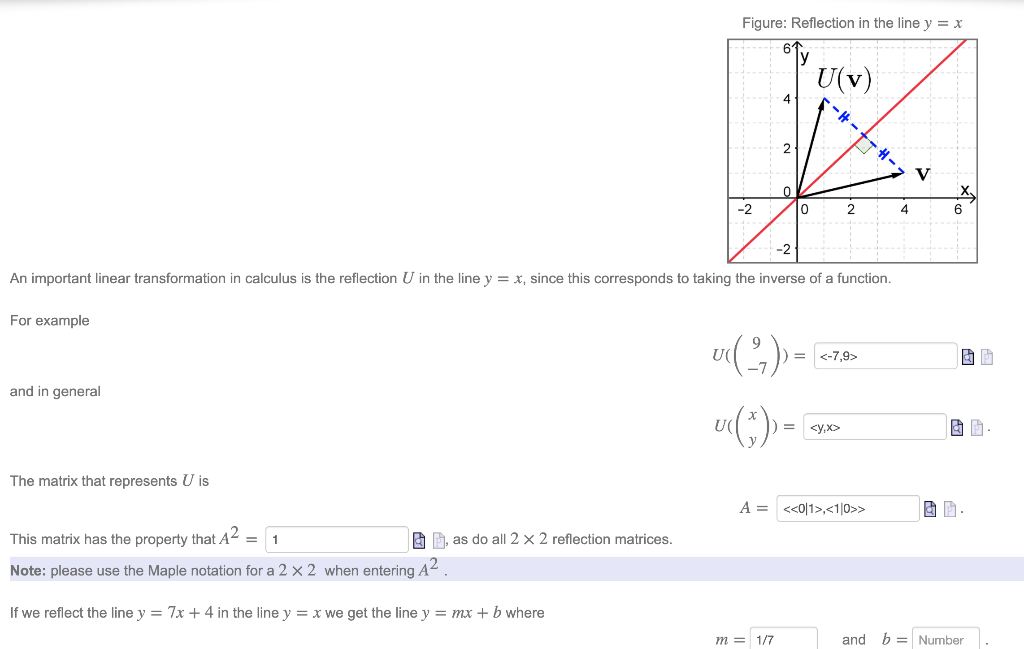



Figure Reflection In The Line Y X 61 U V 4 2 Chegg Com



Reflection Definition Reflection In The Coordinate Plane



Mirror Lines Can Be Placed Anywhere You Just Reflect



Reflection In Geometry Explanation And Examples




Reflection Transformation Matrix
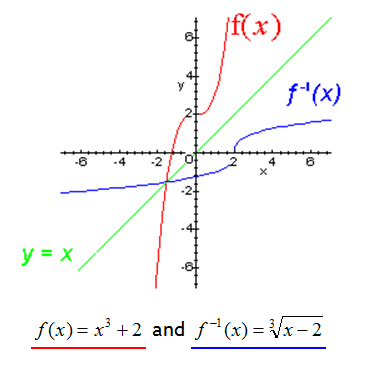



Inverse Functions Example 1




Reflection Over The X And Y Axis The Complete Guide Mashup Math



Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Reflection Over The Y X Line Youtube




Gch12 L1
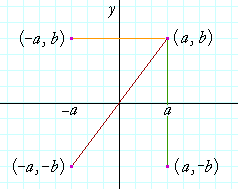



Reflections Of A Graph Topics In Precalculus




Reflection Mathbitsnotebook A1 Ccss Math




Transformation Rules Flashcards Quizlet



1
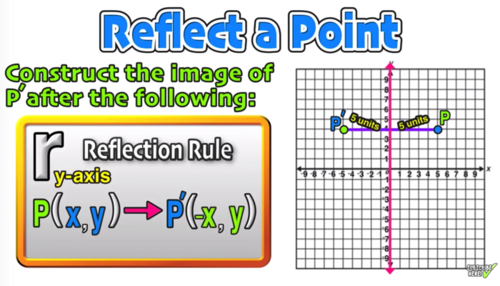



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection In The Line Y X Geogebra




Reflection Mathbitsnotebook A1 Ccss Math
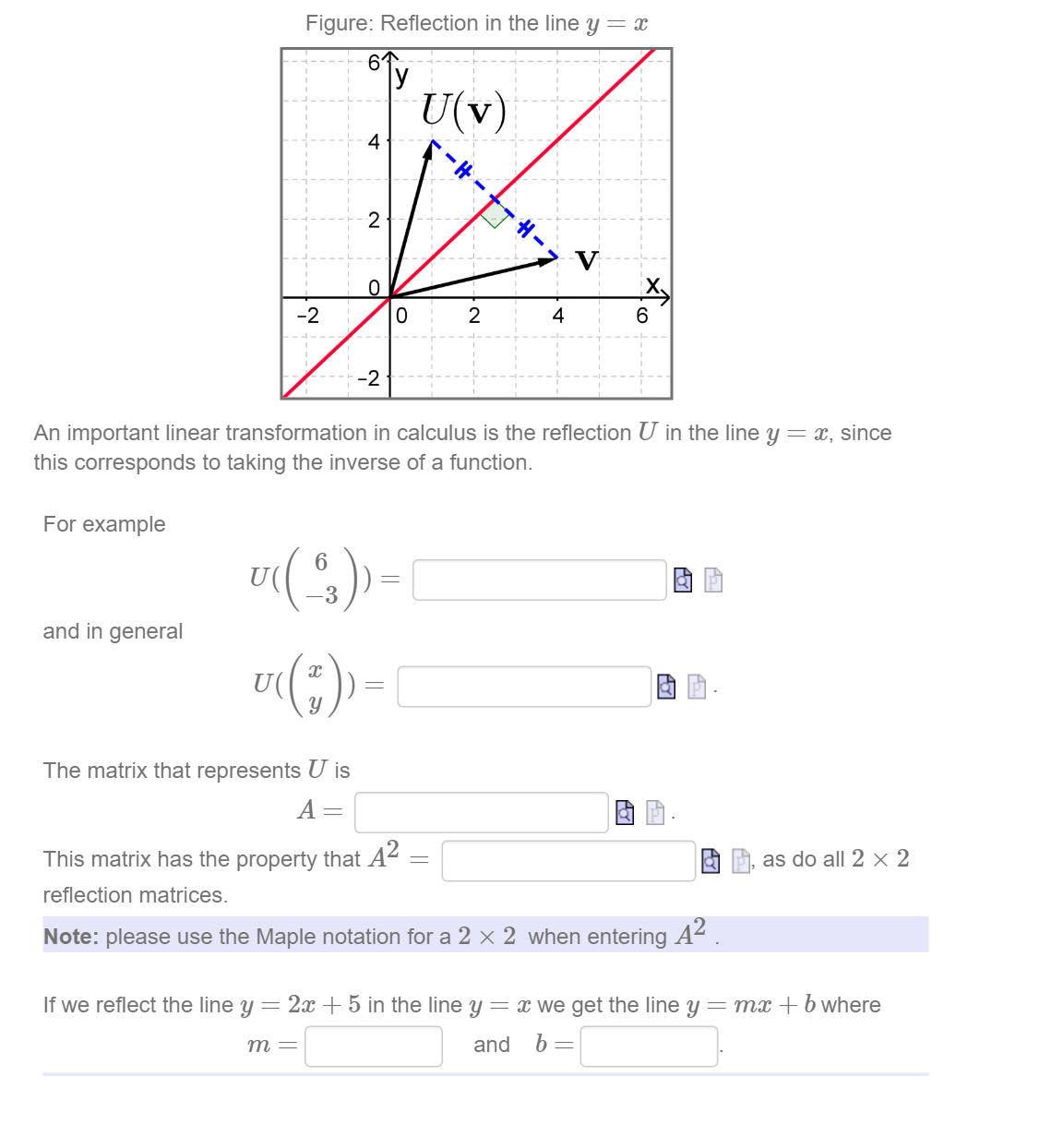



An Important Linear Transformation In Calculus Is The Chegg Com
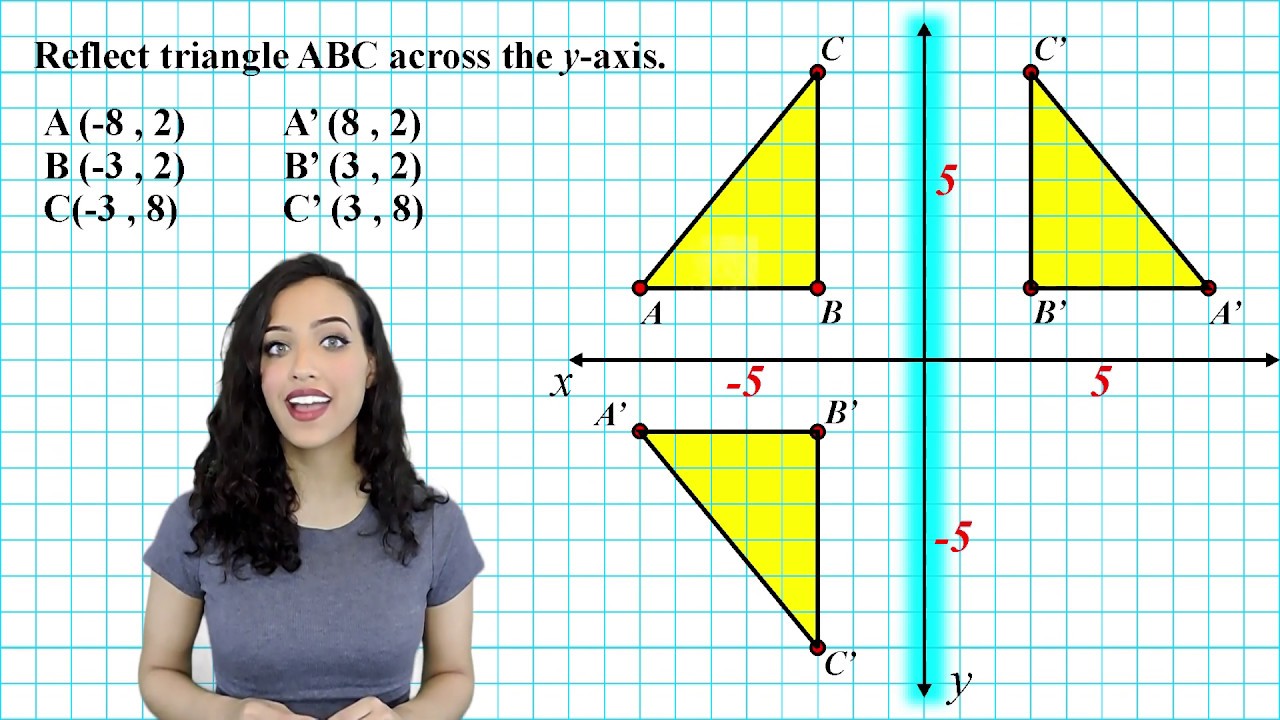



Reflection Across The X And Y Axis Youtube




What Is A Line Of Reflection Printable Summary Virtual Nerd



Www Woodbridgeraiders Net Pdf Learning Opportunities Woodbridge High School April 14 30 Math 04 14 04 24 Geometry Pdf



0 件のコメント:
コメントを投稿